一、前言

         Piaget指出學童的認知發展有四個階段，國小高年級學童的發展階段正處於具體操作期逐漸轉為形式操作期的階段，在學習上的型態從具體的實物幫助其思考漸漸轉變為脫離實物，而使用直接思維的方式，除了使用從邏輯形式解決具體的問題，也發展可以邏輯的形式解決抽像的問題，更進一步發展出統整的思考。

        建構主義的哲學觀中提及「新的學習是建立在舊有的學習經驗基礎上」，希望學習者能夠透過舊有認知學習經驗進行有意義的學習。在數學學習上，主張學習者能夠先理解單元目標的概念，再進行數學解題的學習。這樣的觀點，提供現場教學者在設計教學活動與實施上很大的啟發。每次新的教學單元，教學者必須要探求與瞭解學生的先前相關的學習經驗，就是要明瞭學習者的先備知識（acke knowledge），才能夠設計並採取適合學習者學習的教學活動，引導學習者從舊有經驗概念中進行新概念的學習。

        基於從教育心理學的觀點與教育哲學觀點之下，教學者在教學中可透過喚起學習者的舊經驗，待其了解概念後，再逐次引導學生發展解決問題的想法，及對所得到的答案作解釋。從喚起學習者舊有經驗的教學活動中，引導學童能建構數學解題的規則，並透過實際練習後能自動化。

二、學習者在分數除法容易產生的問題

        一些學者認為學習者會解分數除法問題，但不一定了解分數除法的概念，學童可能只是熟記「除數顛倒－相乘」的規則。而國內學者李源順（2005）也發現到國內、外高年級教師亦大都以「除數顛倒－相乘」的規則來進行分數除法的教學。基於社會建構主義觀點，教學者希望學童能進行有意義的學習。也就是說，教學者應該幫助學習者先了解其學習新概念之後再來進行解題。所以教學者在進行教學時，要能夠先對教學的內容有所理解，並以適當的方法引導學習者理解概念。

        在Sinicrope, Mick, & Kolb (2002) 的研究也從新概念學習內容作分析，將分數除法的概念學習進行分析，並分進行分數除法的教學，以等分除（除以整數）、包含除（除以分數）、和乘法逆運算，其中分數除以分數的問題中也是引導學習者舊有學習經驗出發，設計學習分數除法概念的引導教學活動。

        在上述研究顯示，學習者在學習分數的除法之概念時，較容易於代分數的除法及數字較大的題目中產生錯誤，是因為學習者並未將先備學習概念（因數與倍數）融入到新的學習中。因此教學者可以引導學習者提取先備概念，安排於新的學習活動中。

三、從分析教材內容、喚起經驗改進分數除法教學實務

        在102學年度康軒版教科書六上數學教材第二單元之學習主題為分數的除法，主要學習內容為：認識最簡分數、能解決同分母分數的除法、整數除以分數、異分母分數的除等概念。在最簡分數、同分母的分數的除法、整數除以分數，分母相同等概念部份，學習者較少產生另有概念；然而在異分母分數的除法的學習過程，學習者較容易產生另有概念，在以往研究發現，大部份教學者是以口訣方式「除數顛倒－相乘」教導學習者學會分數除法的運算模式，學習者並非真正理解口訣所代表的真實意義。

        面對這樣的情形，教學者可以從基本的分數除法舊有學習經驗進行教學，喚起學習者先前學習公倍數的概念、除法算式與分數表示方式轉換的概念，建立異分母的分數除法計算方式新概念，而瞭解異分母的分數除法的演算方式。如下：

分數分母的通分後，分子除以分子、分母除以分母的概念，如

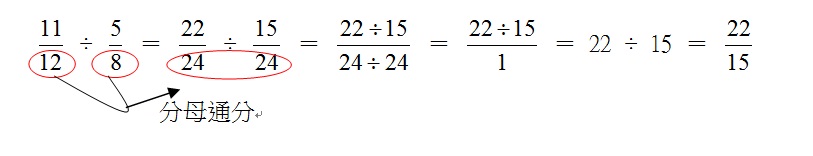
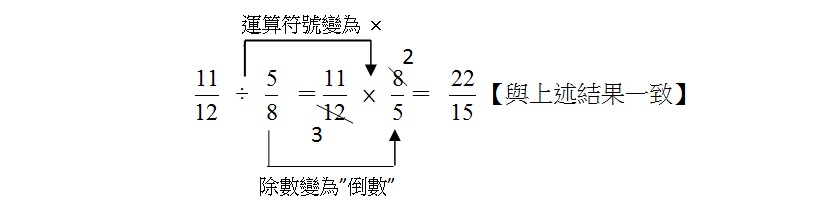
當學習者建構了異分母的基本除法概念演算，教學者可進一步從兩個分數的分母通分使用兩分數相乘通分找公倍數的舊有經驗，對演算式作一相對應的解說，如

        學習者將會發現原本的題目已經從除法的演算式轉變為乘法的算式，並且發現除數已經轉變為倒數後和原先的被除數相乘。學習者理解演算推理的方式才算是真正的理解，而非僅以記憶演算（分數的除法，被除數不變，÷ 運算符號變為 × 後，除數上下顛倒）的方法而已。雖然這樣的推理演算方式對學習者是屬於抽像思考的模式，但是依據Piaget指出六年級的學習者已進入形式操作期，可以進行抽像的思考，所以教學者可以引導學習者建構推理式的抽像思考，幫助理解「除數顛倒－相乘」的抽象理解。當學生比對相關算式演變內容後，可以順暢運用算式中的結構進行轉換的分數除法的運算。

四、學習者在小數除法容易產生的問題

       根據國科會相關的教學研究指出，學習者在處理小數除法計算問題時，對沒有餘數的題目，表現得比有餘數的題目來得好，因為學習者在進行小數除以小數計算時，在小數單位量轉換中，對商和餘數分別代表的意義不清楚，也就是對餘數及商之單位量解讀產生錯誤，所以不是忽略了餘數的小數點，就是將餘數的小數點對齊移位後的被除數小數點，這顯示許多學童對於單位量運用之意義沒有完全瞭解。

        劉曼麗（2008）的研究指出，小數除法的直式計算與整數除法直式計算雷同，差別僅在於小數點的處理，很多教師便要求學生直接記憶算則，學習者在不明就裡的情況下，常常弄不清楚商與餘數的小數點到底要對齊被除數移位前的小數點還是移位後的？

        如同分數除法的教學一樣，教學者僅以計算技巧的口訣教學，並非幫助學習者理解概念，建構真正的理解。一般教學者在教導學習者學習小數的除法是以單位量的概念教學，而忽略了從學習者先前整數的除法或分數的除法之學習概念引導新概念之學習。

五、從分析教材內容、喚起經驗改進小數除法教學實務

        康軒版六年級上學期第四單元主題為小數除法，單元的教學目標為解決小數（整數）除以小數的問題，而先備概念為小數除以整數、整數除以整數商為小數的除法問題，劉曼麗（2008）指出學習者在此單元的學習容易產生的迷失概念為，不知道如何處理商及餘數小數點位置的問題？通常教師在引導解決的方法是從單位量（幾個0.1或是幾個0.01）的引導活動著手，或是以小數點退位的口訣（以除數為標準退位，餘數要和新的小數點位置對齊），引導學習者進行小數轉換為整數直式的解題活動。

如：

1.6 ÷0.2 = 16 個0.1÷2個0.1

1.6為16個0.1

0.2為2個0.1

因此可先將1.6視為16，而0.2視為2整個除法算式可先當作是

16 ÷2 ＝8

因為皆是以0.1為單位量。

        上述的教學活動即為引起舊有學習經驗，是借助整數除法的經驗解決小數除法的問題。因為單位量的判準為「0.1」，題型剛好是除數與被除數的小數位數恰為小數點一位，所以被除數與除數可以轉換為學習者熟悉的整數除法算式。根據劉曼麗（2008）的研究顯示，將被除數與除數皆轉換為單位量為0.1整數除法的算式後，學習者計算之正確率可以提升。

        雖然研究上以0.1單位量解說小數的除法方式可以提升學習者解題的正確率，但是教學者還可以從教材第二單分數的除法的內容，輔以四年級分數與小數的轉換學習經驗，改變引導教學方式，以分數除法舊有經驗解說除法算式的轉換，並理解單位量為0.1的概念。

如：

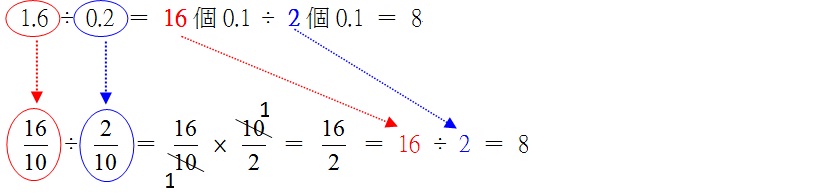
但是在面對另一題型時，當被除數的小數位數比除數小數為多時，課本介紹的學習活動即為以『除數』單位量為判斷標準

如：

8.51 ÷2.3

以除數單位量為判準：因為除數是小數一位，

即將2.3是為23個0.1

因此被除數須視為85.1個0.1

直式算式的表示方式即為

        這樣使用單位量0.1的判準引導活動，除數可以轉換為整數，而被除數卻仍然存在著小數，在學習經驗中是比較不熟悉的經驗，學習者容易產生混淆因而計算正確率偏低。如果可以轉化為整數除法學習經驗，學習者更容易接受。於是教學者可以改變單位量，改以單位量為0.01

因此

8.51擴分100倍後，可以視為851個0.01

除數2.3擴分同樣100倍後，可以視為230個0.01

原來算式即轉變為  851 ÷230 ＝3.7

類似這樣的引導活動，可以降低學習者小數點位置迷失概念的產生。

        從上述兩種使用不同單位量轉換為整數除法的概念，學習者知道單位量的使用，但是可能還不太理解如何選定判準的單位量？為何使用單位量的判準可以將小數除法算式轉換為整數除法的概念？教學者可以運用另一個學習經驗，就是從分數擴分的概念及分數除法的概念引導，除法通常可以使用分數的表示方式，

如：

再將其轉換為除法算式 851 ÷230

學習者容易發現分子與分母皆 ×100，擴大100倍，即以0.01為單位量。

或是轉換為分數除法算式：

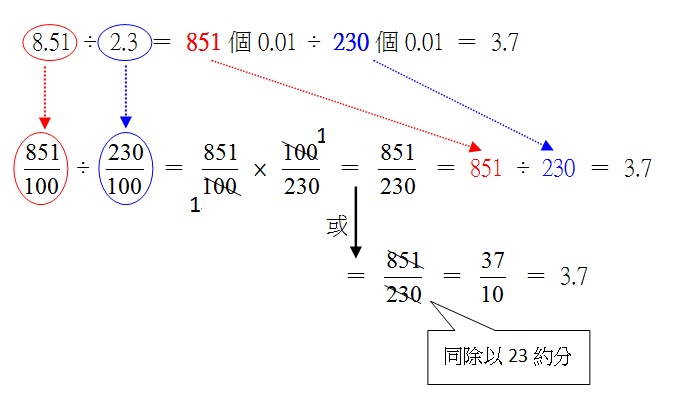
        從舊有學習經驗讓學習者理解選擇單位量的概念就是分數中擴分的概念，而且不再僅以除數的小數位數為單位量判準，而是可以檢視除法算式中較多位小數的數（可能是除數，亦可能是被除數）當作選定單位量的判準，

如

六、結語

         以上所討論的僅只於現場教學者在教學過程中，秉持建構主義哲學觀點「新的學習是建立在舊有的學習經驗之基礎上」，以及接受皮亞傑指出學童認知發展階段的假設，國小高年級學童進入形式操作期階段，可以嘗試促進學童抽像思考的教學，引導學習者在學習過程中，從舊有的學習認知經驗，發展新概念的學習理解。在九年一貫數學學習領域課程綱要中，分數除法概念性與小數除法的概念學習對學童而言是一種較為抽象的思考方式。從課程教材的內容分析發現，分數除法和小數除法的程序性知識很重要，學習者要記憶一般教師教學的口訣是容易的，但是要真正理解分數除法與小數除法的程序性概念知識是不容易的。因此，透過教學者對教學教材的內容分析，並找出學習者舊有學習經驗，，在教學過程中充分考量學習者之舊有認知知識，藉此喚起學習者舊有學習經驗，完成新的概念之理解。