創刊日:100 年 6 月 10 日
發行人:教育局局長
出版者:臺中市政府教育局
地址:42007 臺中市豐原區陽明街 36 號
電話:04-2228-9111(代表號)
臺中市教育電子報自民國 100 年 6 月起,每月 10 日發行一期,為教育夥伴提供更快速便捷與寬廣詳實之教育資訊 ,歡迎各界關心教育訊息之舊雨新知,上網免費訂閱,並請廣為推廣宣傳。
數學,在學生心中恐懼科目之排行榜是位居榜首的地位,主要原因是它與其他科目不同,它並不是背多分而是「想多分」,當你真正了解它的特性與奧祕的話,你就可以晉升到「享多分」的境界。
為什麼數學一直是學生恐懼的科目呢?很多人以為多花時間練習就可以進步,結果考試成績卻不如預期,第二次再試看看,結果還是一樣,如此一連串的打擊,便開始失去學習信心,認為再多花時間還是一樣,不如把時間花在其他的科目上,至少可以彌補數學上的缺口。
數學並不是多算就一定會,我常喜歡跟學生開玩笑說:「如果按照你的說法,從現在開始,我每天跟我家的寵物說話,幾年後我就可以跟牠溝通囉!」當然這是不太可能,數學也是一樣,如果一開始定義及概念沒搞懂,算再多題目也一樣不會,就算你會解這題,一樣的題型改個問法可能就不會了,如果要記每個題目,試問要記多久?才可以把全部的題目都記完?我相信答案是永永遠遠!
【其實數學並不難】,這句話學生聽到後應該會說:「你是老師,當然不會覺得很難啊!」說句肺腑之言,當你了解它後,就會跟我一樣,熱愛數學到癡狂的地步!要學好數學不外乎幾點:記憶、理解、聯想、練習。
所謂記憶,不是要記它的題目,而是要記它的定義,例如:何謂絕對值,當你問學生時,很多同學就會說:「絕對值出來都是正的」,我就會反問:「那請問零的絕對值是多少」,他們就會回答:「零」,既然絕對值出來都是正的,而零既不屬於正數也不屬於負數,出現了非常大的矛盾點,學生的問題相對發生。由此可見,學生往往只是學,並沒有學完整、學徹底,正確的絕對值定義應該是:「一數字a的絕對值為此數a與原點的距離,以│a│表示之。」既為距離就不會有負的可能。
當認識定義後,接著要理解從它推導出來的相關定理,了解推導過程的證明,能更進一步地加深印象。而學數學不可或缺的本質之一就是聯想,要學著天馬行空地去想,解題的方法不是只有一種,要試著聯想是否有其他的方法可以解題,或許在這樣思考的過程中,對題目會有不一樣的體會。當做到上述幾點後,接著練習題目,或許你會覺得算題目不一定有用?為什麼現在又要練習算題目?事實上,兩者之間是有其差異性,一種是不了解內容,盲目的、拼命的算;另一種是了解它的架構之後才練習。盲目地硬算,就算練習很多仍然不懂,但當你了解它的架構,練習卻是加深印象及熟練題型。
許多人沒辦法把數學學好是因為學習的方法錯誤或是學習的態度不夠嚴謹,每個人的學習方法不同,你應該要去找到一個屬於自己的學習模式,那這又跟學習態度有什麼關係?這關係可大的呢!數學為什麼被稱為科學之母,因為它非常嚴謹,一個定理可以出現,它的推導證明過程必須經過非常多的檢驗再檢驗之後才能成立,所以在證明的過程必定是要非常的細心,一個地方有個小錯誤就會導致結果沒辦法出現,所以解題的過程必須要非常的嚴謹、細心,這個時候學習的態度就非常的重要,成敗的關鍵就在於對待它的態度,態度不只決定你的高度,也決定分數的高度。
一開始我也提到學生常常數學學不好是因為沒有信心、自信,為什麼會沒有信心?因為分數低!當然,同儕之間一定會比較,但我們並不需要跟人比,每個人是獨立學習的個體,人比人氣死人,我常常看到很多學生拿到考卷之後愁眉苦臉,對自己的實力與努力開始懷疑,從此就造成之後數學不進反退的現象。愁眉苦臉分數就能夠回來嗎?答案是否定的,良好的心態應該是要去想考不好的問題出在哪裡,基本上可以粗分為兩類:第一類是會寫但寫不完,第二類是寫完了但是錯很多,第一類的學生可以在平時多練習題目,訓練自己的算算能力,而第二類的學生可以在分成兩種,第一種是粗心,第二種是定義、定理搞混導致的,第一種要在解題時放慢速度,減少出錯的機率,第二種比較麻煩,必須要再詳細的將所學的定義定理讀懂。
每個人都有一套屬於自己的解題及念書方法,這裡就要分享我的解題方法與學數學的方法,解題我習慣用逆推法來思考,以下我舉國三上的第二單元的圓來作例子: 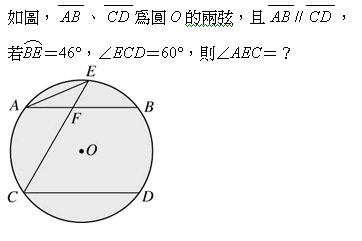
看到題目,第一步我會去看題目要求什麼,接著將它步驟一個一個逆推回去,題目要求∠AEC的度數,因為∠AEC是圓周角,度數是︵AC度數的一半,所以只要知道︵AC弧就可以求∠AEC,那︵AC又要怎麼求呢?這就要看題目所給的條件來推導,題目給了幾個條件,//、︵BE=46°和∠ECD=60°,其中//可以得︵AC=︵BD,∠ECD(圓周角)=60°可以得︵BD+︵BE=∠ECD的兩倍=120°,又︵BE=46°,所以最後可以得到︵BD=74°,進而推得答案∠AEC=74°/2=37°
我解題的思考方向: 題目求∠AEC→要求︵AC→先求︵BD→∠ECD是圓周角可以得到︵BD+︵BE的值,而且︵BE已經給定,所以求得︵BD
題目解題的步驟:
∠ECD(圓周角)=(︵BD+︵BE),︵BE=46° → ︵BD=74° → // → ︵AC=︵BD=74° → ∠AEC(圓周角)=︵AC=×74°=37° 由所求的問題逆推回一開始要求的方法常常被用到,尤其是當你一開始毫無頭緒的時候,這個方法會幫助你很多。
除了解題技巧,最後要分享如何有效率的學習數學,上課前必須準備草稿紙,,接著要牢記三步驟:專心聽、快速寫、慢慢抄。上課老師講解的重點不再解題的步驟,而是破題的方法,這個時候專心聽是非常重要的,千萬不要邊聽邊寫,當題目講解完後,老師會寫下一題的題目,在這段短暫的時間,必須很快速的將老師講解的過程寫到草稿紙上,回家後將草稿紙上所寫的內容,再慢慢地抄到上課的講義裡,若有自己的想法也可以加以敘述。相信,這比上課邊抄邊上,回家後完全沒有印像的學習法好很多。考前複習時,一本是匆促寫上、字跡潦草的內容,另一本是書寫工整,而且上面還加上自己註記與見解的講義,我相信應該沒有人想用字跡潦草,內容有些還看不懂的講義。 如此一來,不僅增進學習數學的信心,而且常常沉浸「享多分」的境界。
創刊日:100 年 6 月 10 日
發行人:教育局局長
出版者:臺中市政府教育局
地址:42007 臺中市豐原區陽明街 36 號
電話:04-2228-9111(代表號)
臺中市教育電子報自民國 100 年 6 月起,每月 10 日發行一期,為教育夥伴提供更快速便捷與寬廣詳實之教育資訊 ,歡迎各界關心教育訊息之舊雨新知,上網免費訂閱,並請廣為推廣宣傳。
蔣偉民局長
蘇美麗科長
課程教學科王柏鈞股長、詹益榮老師;南屯區永春國小蕭俊勇校長、王清峰主任
教育領航:西屯區上石國小劉益嘉校長、黃薏蒨組長;北區太平國小曾娉妍校長、彭文欣主任;
教育動態:中區光復國小張毅宏校長、蔡牧耕主任、林靜鶯組長;東勢區新盛國小譚至皙校長、李曉玲主任;
校園風情:北勢國中林宏泰校長、劉芳如主任;西屯區東海國小林筆藝校長、張凱棠主任、楊琮渝老師;
人物特寫:西區大同國小廖曉柔校長、謝俊宏主任;大里區大元國小張曡今校長、王怡月組長;
焦點話題:清水國中鐘文生校長、洪嘉祥主任、王詠婕老師;烏日區旭日國小吳桂芬校長;
教學錦囊:四箴國中方玉婷校長、董家琳組長;大里區益民國小洪翠芬校長、吳相儒主任;
教育夥伴:西區忠信國小黃美樺校長、施政旻主任;清水區槺榔國小王勝忠校長、林麗玉主任、枋宛臻組長;
書香共聞:大甲區順天國小陳素萍校長、顏淑菁主任;大雅區三和國小李勝億校長、王昭明主任;
行政組:南屯區永春國小蕭俊勇校長、王清峰主任;
網路服務:課程教學科黃晉恩股長;