在上數學課的過程中，常會有學生問我，「老師，學那麼多數學有甚麼用？日常生活又用不到，說實在話，只要會數學的四則運算，就足夠了」面對這種問題，發現大家真的對數學教育誤解，數學的運算技巧不是數學教育的目的，而是工具。數學教育的目的就是要訓練學生解決問題的能力。

  趨勢大師大前研一指出「解決問題的能力」是未來生存的三大技能之一，而人不是憑空就能針對問題的重點，提出最佳的解決方案。人必須訓練此能力，最佳方法就是數學教育一充分了解情況(題目)，在有限的現實條件下(已知)，利用手邊擁有的資訊(數學運算技巧)，提出最佳解決方案(解題)。每一道數學題都是訓練上述的思考步驟，進而內化它，隨時面對問題、解決問題。

  在數學教育中,為使學生擁有更多的解題資源，對於數學各種多元的符號及運算等，則要進行教學,精熟練習也是必要的。當學生面對有些枯燥但又必須學習的數學,激發學習興趣，生活化與情境化的教學內容,正是用來吸引學生的棒棒糖。

  以下提供幾則個人教學的小技巧：

  (1) 生活實例的適當舉例:

例如：「一元一次方程式」在解釋抽象符號ｘ時，適當的舉例就很重要。

例如：一包口香糖代表ｘ兩包口香糖代表2x

2ｘ＋3　即代表兩包口香糖加3條口香糖

不會等於五條，這樣四則運算也易進行教學。藉著具體的事物來連結抽象的符號ｘ，進入代數的世界就更容易了。

  (2)摺紙在幾何教學的應用

應用摺紙---依線段的兩點對折可以得到中垂線，兩個鄰邊，邊和邊對折可以得到角平分線。高，中線一樣可以透過折紙觀察。內心，外心，重心，正三角形，皆可以用折紙來呈現。筆者的老師之前透過摺紙建構出空間的立體坐標軸。

抽象的三角幾何，透過動手做.變具體了.加上教師引導.基本觀念就易建構完成。

  (3)迷思概念的講解：

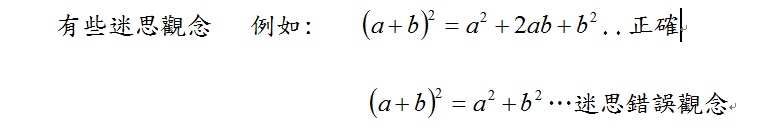
透過圖形的分割技巧，就很容易看出。因此在第三冊1-1的教學上.圖形的說明.

是必要性的，只用分配律導公式，學生比較沒有感覺。

  (4)幾何不行找代數，代數不行找幾何

例1:質數除了1和本身以外沒有別的因數，這是代數上的定義。

  質數p=1Xp轉換成幾何就是利用1X1的正方形紙板，只可以拼成唯一的長方形。

   長寬為(1.P)或(P.1)

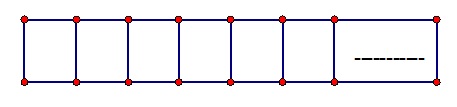
例2:一元二次方程式 

                    3x+y=100

                    2x+3y=90

轉換成情境教學.就是可以設計成一塊紅磚.長度為X公分.寬為y公分

3x+y=100  情境設計為

三塊橫放磚頭加一塊直立磚頭總長度為100公分

2x+3y=90

情境設計為

兩塊橫放磚頭加三塊直立磚頭總長度為90公分

在利用磚塊倍數的方法

                    3x+y=100-->6x+2y=200

                    2x+3y=90-->6x+9y=270

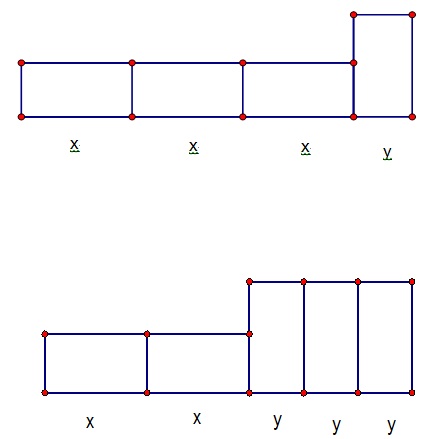
導入加減消去法消去一個未知數的概念，算出磚頭的長，寬即x，y 值

在教學中，盡量透過情境化，讓學生先接受，熟練它，最後再應用。

   教學的目的不是只趕進度，有教就好，而是品質得提升，教學的成敗，教和學各一半，建構概念是教師的責任；精熟和應用是學生的責任。多種策略，多種教法活用，讓學生在面對問題，能夠有一套標準的思考流程，這種內化的成功就是數學教育的成功。